쭉쭉 풀어보자.
* 차량 번호판 1 (mid) : 조건을 만족하는 차량 번호판 개수를 구하는 문제다.
16968번: 차량 번호판 1
00부터 99까지 총 100가지 중에서 00, 11, 22, 33, 44, 55, 66, 77, 88, 99가 불가능하다.
www.acmicpc.net
- 같은 글자가 두 번 연속해서 나타나면 안 된다는 조건은, 무조건 그 앞의 숫자랑만 다르면 되는 거니까 맨 앞에는 n, 그 다음부터는 쭉 n-1이라고 보면 된다.
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int main()
{
int ans = 1;
string num;
cin >> num;
int cC = 0, cD = 0;
int ch = 26, d = 10;
for (int i = 0; i < num.size(); i++) {
if (num[i] == 'c') {
if (cC == 0) {
ans *= ch;
}
else {
ans *= (ch - 1);
}
cC += 1;
cD = 0;
}
else {
if (cD == 0) {
ans *= d;
}
else {
ans *= (d - 1);
}
cD += 1;
cC = 0;
}
}
cout << ans << '\n';
return 0;
}- 어렵지 않게 구현하긴 했는데, 재귀로 푸는 연습을 좀 해야할 것 같다. 이런 단순한 문제도 재귀로 구현할라고 하면 은근 헷갈린다..
#include <iostream>
#include <string>
using namespace std;
int go(string &s, int idx, char last) {
if (s.size() == idx) {
return 1;
}
int start = (s[idx] == 'c' ? 'a' : '0');
int end = (s[idx] == 'c' ? 'z' : '9');
int ans = 0;
for (char i = start; i <= end; i++) {
if (last != i) {
ans += go(s, idx + 1, i);
}
}
return ans;
}
int main()
{
string num;
cin >> num;
cout << go(num, 0, ' ') << '\n';
return 0;
}- 훨씬 깔끔하게 구현할 수 있다. 어렵더라도 재귀로 구현하려고 노력해보자. 그래야 더 어려운 문제도 푼다.
* 양념 반 후라이드 반 (mid) : 반반 치킨을 활용해 치킨 가격의 최솟값을 구하는 문제다.
16917번: 양념 반 후라이드 반
현진 치킨에서 판매하는 치킨은 양념 치킨, 후라이드 치킨, 반반 치킨으로 총 세 종류이다. 반반 치킨은 절반은 양념 치킨, 절반은 후라이드 치킨으로 이루어져있다. 양념 치킨 한 마리의 가격은
www.acmicpc.net
- 개수가 딱 맞아 떨어지는 게 아니라, 최소 x마리, y마리 이런 식이므로 개수가 오버가 되어도 최솟값이기만 하면 된다. 문제 자체는 그리 어렵지 않았다.
- 일단 반반 2개가 후1+양1보다 비싸면 반반을 활용할 가치가 없으므로 그냥 따로 시키면 된다. 반반이 더 싸면 일단 반반으로 짝 맞춰서 구입한 후, 각각 남은 것을 구매할 때 한번 더 반반과 비교해서 싼 걸로 시킨다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int ans = 0;
int a, b, c, x, y;
cin >> a >> b >> c >> x >> y;
if (a + b < c * 2) {
ans = a*x + b*y;
}
else {
int m = min(x, y);
ans += c * 2 * m;
x -= m; y -= m;
if (x > y) {
if (a*x < c * 2 * x) ans += a*x;
else ans += c * 2 * x;
}
else if (x < y) {
if (b*y < c * 2 * y) ans += b*y;
else ans += c * 2 * y;
}
}
cout << ans << '\n';
return 0;
}
* 로마 숫자 만들기 (mid) : 복잡하게 생각하다가 꽤나 헤맸던 문제다.
16922번: 로마 숫자 만들기
2, 6, 10, 11, 15, 20, 51, 55, 60, 100을 만들 수 있다.
www.acmicpc.net
- 포인트는 순서에 상관 없이, 그 자리의 값을 더해주기만 하면 된다는 거다. 그럼 차례로 나열할 필요 없이 그냥 개수만 세어줘도 무방하다.
- 4가지 수지만, 3가지만 정해지면 굳이 4번째 수를 다 찾아볼 필요 없이 n에 3가지 수의 합을 빼주면 된다. 그럼 O(n^3) 안에 문제를 해결할 수 있다. n의 범위도 20까지여서 문제 없다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
bool check[1001];
int main()
{
int n;
cin >> n;
int ans = 0;
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n - i; j++) {
for (int k = 0; k <= n - i - j; k++) {
int l = n - i - j - k;
int sum = i + j * 5 + k * 10 + l * 50;
check[sum] = true;
}
}
}
for (int i = 1; i <= 1000; i++) {
if (check[i]) ans += 1;
}
cout << ans << '\n';
return 0;
}- 아이디어가 떠오르지 않으면 한참 헤맬 수 있는 문제다. 요령을 잘 기억해두자.
* 십자가 찾기 (mid) : 십자가 모양 만으로 주어진 그림을 그릴 수 있는지 판별하는 문제다.
16924번: 십자가 찾기
십자가는 가운데에 '*'가 있고, 상하좌우 방향으로 모두 같은 길이의 '*'가 있는 모양이다. 십자가의 크기는 가운데를 중심으로 상하좌우 방향으로 있는 '*'의 개수이다. 십자가의 크기는 1보다 크
www.acmicpc.net
- 우선 단순하게 차근차근 생각해서 그냥 풀었다. 일일이 확인해주고, 그대로 복붙해서 원래 그림과 같으면 저장한 좌표와 십자가 크기를 출력해준다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct id {
int x, y, size;
};
int main()
{
int n, m;
cin >> n >> m;
vector<vector<char>> a(n, vector<char>(m));
vector<vector<char>> check(n, vector<char>(m,'.'));
vector<id> ans;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> a[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (i - 1 < 0 || i + 1 >= n || j - 1 < 0 || j + 1 >= m) continue;
if (a[i][j] == '.') continue;
int size = 1;
while (i - size >= 0 && i + size < n && j - size >= 0 && j + size < m) {
if (a[i - size][j] == '*' && a[i + size][j] == '*' && a[i][j - size] == '*' && a[i][j + size] == '*') {
check[i - size][j] = '*';
check[i + size][j] = '*';
check[i][j] = '*';
check[i][j - size] = '*';
check[i][j + size] = '*';
ans.push_back({ i+1,j+1,size });
size += 1;
}
else {
break;
}
}
}
}
if (a == check) {
cout << ans.size() << '\n';
for (int i = 0; i < ans.size(); i++) {
cout << ans[i].x << ' ' << ans[i].y << ' ' << ans[i].size << '\n';
}
}
else {
cout << -1 << '\n';
}
return 0;
}- 근데 좀 오래 걸렸다. 정답 코드를 참고해서 코드를 좀 개선했다. 일단 굳이 char형으로 복사해서 메모리를 낭비할 필요가 없으므로 bool 형으로 바꿔줬다. 또한, 십자가를 확인할 때 위에서는 작은 것부터 일일이 다 확인해서 저장했는데, 어차피 큰 십자가가 작은 걸 다 포함하니까 해당 위치에서 가장 큰 십자가만 구하도록 구현했다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct id {
int x, y, size;
};
int main()
{
int n, m;
cin >> n >> m;
vector<vector<char>> a(n, vector<char>(m));
vector<vector<bool>> check(n, vector<bool>(m,false));
vector<id> ans;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> a[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (a[i][j] == '*') {
int l = 0;
for (int k = 1;; k++) {
if (i - k >= 0 && i + k < n && j - k >= 0 && j + k < m) {
if (a[i + k][j] == '*' && a[i - k][j] == '*' && a[i][j - k] == '*' && a[i][j + k] == '*') {
l += 1;
}
else break;
}
else break;
}
if (l > 0) {
ans.push_back({ i + 1,j + 1,l });
check[i][j] = true;
for (int k = 1; k <= l; k++) {
check[i - k][j] = true;
check[i + k][j] = true;
check[i][j - k] = true;
check[i][j + k] = true;
}
}
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (a[i][j] == '*' && check[i][j] == false) {
cout << -1 << '\n';
return 0;
}
}
}
cout << ans.size() << '\n';
for (int i = 0; i < ans.size(); i++) {
cout << ans[i].x << ' ' << ans[i].y << ' ' << ans[i].size << '\n';
}
return 0;
}- 코드 상으로는 큰 차이가 없어보이지만 속도 면에서는 많이 차이가 났다. 왠만하면 빠르게 구현해야하지 않것어?
* 나3곱2 (mid) : 스스로 푼 것도 괜찮았지만, 요령을 알면 훨씬 쉽게 풀 수 있는 문제였다.
16936번: 나3곱2
나3곱2 게임은 정수 하나를 이용한다. 가장 먼저, 정수 x로 시작하고, 연산을 N-1번 적용한다. 적용할 수 있는 연산은 두 가지 있고, 아래와 같다. 나3: x를 3으로 나눈다. x는 3으로 나누어 떨어져야
www.acmicpc.net
- 3으로 나누기, 2로 곱하기 연산 중 하나를 선택해 해나가고, 그 순서를 섞은 뒤에 원래 순서를 맞추는 문제다.
- 처음엔 구조체를 선언해서 in, out을 지정해줬다. in에는 현재 값을 3으로 나누기 전 수의 인덱스, out에는 2로 곱한 후의 인덱스를 넣어줬다. in이 없으면 첫 수니까, 거기서 출발해서 out이 없는 수까지 쭉 출력해줬다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct game {
int in;
int out;
};
int main()
{
int n;
cin >> n;
vector<long long> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
sort(a.begin(), a.end());
vector<game> check(n);
for (int i = 0; i < n; i++) {
check[i].in = -1;
check[i].out = -1;
}
for (int i = 0; i < n; i++) {
bool cd = false, cm = false;
for (int j = i + 1; j < n; j++) {
if (cd && cm) continue;
if (a[i] * 2 == a[j]) {
check[i].out = j;
check[j].in = i;
cm = true;
}
if (a[i] * 3 == a[j]) {
check[i].in = j;
check[j].out = i;
cd = true;
}
}
}
for (int i = 0; i < n; i++) {
if (check[i].in == -1) {
int idx = i;
while (check[idx].out != -1) {
cout << a[idx] << ' ';
idx = check[idx].out;
}
cout << a[idx] << ' ';
cout << '\n';
break;
}
}
return 0;
}- 이것도 나쁘지 않았는데, 훨씬 직관적인 방법이 있었다. 2로 곱하는 건 수가 계속 커지는 거지만, 3으로 나누는 건 수가 줄어드는 거다. 거기에 3이 하나씩 줄어들기 때문에 3의 개수에 따라 순서를 추측할 수 있었다. 3의 개수에 따라 내림차순 정렬 후, 3의 개수가 같은 수끼리는 2를 곱해서 연산했을 것이므로 오름차순 정렬을 해주면 된다. 정렬로 깔끔하게 해결되니까 이게 훨 나았다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int count3(long long n){
int cnt = 0;
while (n % 3 == 0) {
cnt += 1;
n /= 3;
}
return cnt;
}
int main()
{
int n;
cin >> n;
vector<long long> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
sort(a.begin(), a.end());
vector < pair<long long, long long>> div3;
vector <long long > mul2;
for (int i = 0; i < n; i++) {
if (a[i] % 3 == 0) {
int cnt = count3(a[i]);
div3.push_back({ a[i],cnt });
}
else {
mul2.push_back(a[i]);
}
}
sort(div3.begin(), div3.end(), [](auto &a, auto &b) {
if (a.second == b.second) {
return a.first < b.first;
}
return a.second > b.second;
});
for (auto &p : div3) cout << p.first << ' ';
for (auto &p : mul2) cout << p << ' ';
cout << '\n';
return 0;
}
* 두 스티커 (mid) : 로마 숫자 만들기 문제처럼 요령을 모르면 한참 헤맬 수 있는 문제였다.
16937번: 두 스티커
첫째 줄에 모눈종이의 크기 H, W, 둘째 줄에 스티커의 수 N이 주어진다. 다음 N개의 줄에는 스티커의 크기 Ri, Ci가 주어진다.
www.acmicpc.net
- 스티커를 두 개 붙인다고 할 때 가장 효과적으로 붙일 수 있는 방법은 아래와 같았다.
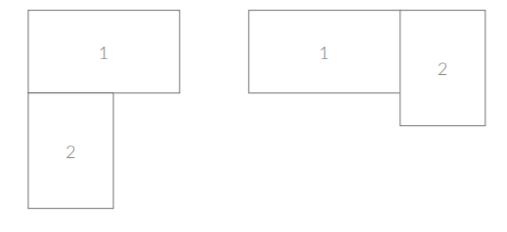
- 이걸 생각을 못 하고 계속 하나는 왼쪽 위 모서리에, 하나는 오른쪽 아래 모서리에 둬야 한다고 생각했다. 이것도 일종의 요령이니.. 잘 기억 해두도록 하자. 이를 바탕으로 구현하는 건 그리 어렵지 않았다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int h, w, n;
cin >> h >> w >> n;
vector<pair<int, int>> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i].first >> a[i].second;
}
int ans = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int r1 = a[i].first; int c1 = a[i].second;
int r2 = a[j].first; int c2 = a[j].second;
for (int ro1 = 0; ro1 < 2; ro1++) {
for (int ro2 = 0; ro2 < 2; ro2++) {
if (c1 + c2 <= h && max(r1, r2) <= w) {
if (ans < r1*c1 + r2*c2) ans = r1*c1 + r2*c2;
}
if (r1 + r2 <= w && max(c1, c2) <= h) {
if (ans < r1*c1 + r2*c2) ans = r1*c1 + r2*c2;
}
swap(r2, c2);
}
swap(r1, c1);
}
}
}
cout << ans << '\n';
return 0;
}- 회전이 가능하다고 했으니, 각각 회전한 경우까지 생각해줘야 한다. 그 중 최대 넓이를 구하면 되겠다.
* 캠프 준비 (mid) : 뭔가 엄청 쉽게 풀렸다.
16938번: 캠프 준비
난이도가 10, 30인 문제를 고르거나, 20, 30인 문제를 고르면 된다.
www.acmicpc.net
- 범위를 확인하고 비트 연산자를 쓰면 되겠다는 생각이 바로 들었다. 그대로 구현하는 건 어렵지 않았다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int n, l, r, x;
cin >> n >> l >> r >> x;
vector<int> a(n);
for (int i = 0; i < n; i++) cin >> a[i];
int ans = 0;
for (int i = 1; i < (1 << n); i++) {
int cnt = 0;
int sum = 0, up = -1, down = -1;
for (int j = 0; j < n; j++) {
if (i&(1 << j)) {
if (up == -1 || up < a[j]) up = a[j];
if (down == -1 || down > a[j]) down = a[j];
sum += a[j];
cnt += 1;
}
}
if (cnt < 2) continue;
if (l <= sum && sum <= r && up - down >= x) ans += 1;
}
cout << ans << '\n';
return 0;
}- 근데 이걸 또 재귀로 구현하더라. 한번 체크하고 넘어가자.
#include <iostream>
#include <algorithm>
using namespace std;
int a[15];
int n, l, r, x;
int go(int index, int count, int sum, int easy, int hard) {
if (index == n) {
if (count >= 2 && l <= sum && sum <= r && hard - easy >= x) return 1;
else return 0;
}
int cnt1 = go(index + 1, count + 1, sum + a[index], min(easy, a[index]), max(hard, a[index]));
int cnt2 = go(index + 1, count, sum, easy, hard);
return cnt1 + cnt2;
}
int main()
{
cin >> n >> l >> r >> x;
for (int i = 0; i < n; i++) cin >> a[i];
cout << go(0, 0, 0, 1000000, 0) << '\n';
return 0;
}- 딱 봐도 코드가 예쁘다. 이해만 잘 하면 생각보다 더 직관적이다. 리턴을 하는 변수를 어디에 선언해줘야 하는지에 대한 감이 아직 덜 잡힌 것 같다. 자꾸 하다보면 익숙해지니까, 재귀 머리 아프다고 자꾸 피하지 말고 쉬운 문제도 재귀로 구현해보는 연습을 자꾸 하자.
-
정리 끝!
'알고리즘 > 백준 알고리즘 강의' 카테고리의 다른 글
| 백준 알고리즘 중급 - 브루트 포스(문제2) (0) | 2020.10.01 |
|---|---|
| 백준 알고리즘 중급 - 이분 탐색 (연습) (0) | 2020.09.07 |
| 백준 알고리즘 중급 - 이분 탐색 (0) | 2020.09.06 |
| 백준 알고리즘 중급 - 정렬 (0) | 2020.09.04 |
| 백준 알고리즘 중급 - 분할정복 (도전) (0) | 2020.09.02 |


