
이미 풀어본 문제가 많아서 빠르게 클리어 했다.
그땐 쩔쩔 맸던 문제들이 지금은 수월하게 풀린다는 것에 놀라기도 했다.
패턴을 찾아도 알고리즘을 짜는 게 은근 까다로워서 고생한 문제도 있었다.
정리 해보자!
-
* 그리디 알고리즘 : 결정해야 하는 그 순간에 가장 좋다고 생각하는 것을 찾아가며 답을 찾아가는 알고리즘이다. 뒤이에 올 것은 생각하지 않고 그때 그때 가장 좋은 선택을 한다고 욕심쟁이라는 이름이 붙었다.
바로 예제로 들어가보자.
* 동전 0 (low) : 가장 간단한 그리디 문제인 거스름돈 문제다. 필요한 동전 개수의 최솟값을 구하면 된다.
11047번: 동전 0
첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 10, 1 ≤ K ≤ 100,000,000) 둘째 줄부터 N개의 줄에 동전의 가치 Ai가 오름차순으로 주어진다. (1 ≤ Ai ≤ 1,000,000, A1 = 1, i ≥ 2인 경우에 Ai는 Ai-1의 배수)
www.acmicpc.net
#include <iostream>
using namespace std;
int main()
{
int n, k;
cin >> n >> k;
int a[10];
for (int i = 0; i < n; i++)
cin >> a[i];
int ans = 0;
for (int i = n - 1; i >= 0; i--) {
if (k == 0) break;
if (a[i] <= k) {
ans += (k / a[i]);
k %= a[i];
}
}
cout << ans << '\n';
return 0;
}- 가장 큰 동전부터 시작한다. 동전이 현재 구하려는 값보다 같거나 작을 때, 동전 값을 구하려는 값에 나눈 값이 사용된 동전의 개수고, 나머지 연산을 한 값이 동전을 사용하고 남은 잔액이다.
- 주의해야 할 점은 동전이 모두 배수 관계일 때만 그리디가 성립한다는 거다. 문제 풀때 그렇다는 것만 알아두자.
* 회의실배정 (mid) : 회의실 사용 시작/종료 시간이 주어질 때 최대로 진행할 수 있는 회의 수를 구하는 문제다.
1931번: 회의실배정
(1,4), (5,7), (8,11), (12,14) 를 이용할 수 있다.
www.acmicpc.net
- 모든 알고리즘 문제가 그렇지만, 특히나 그리디는 문제마다 지니고 있는 핵심 규칙을 생각하는 것이 중요하다.
- 이 문제는 그림을 그려서 문제의 규칙을 유추해볼 수 있다.
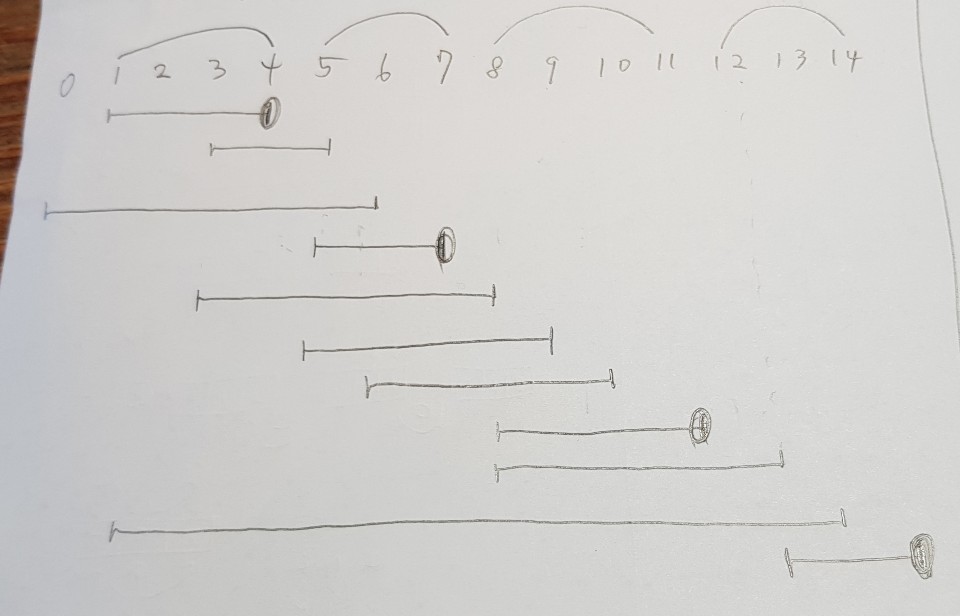
- 먼저 시작하는 회의를 먼저 선택해버리면 언제 끝날지도 모를 녀석을 고를 수도 있다. 끝나는 시간을 기준으로 해야 최대한 많은 회의를 선택할 수 있다.
- 끝나는 시간을 기준으로 선택하되, 그 회의의 시작 시간이 이전 회의가 끝나는 시간보다 먼저여서는 안 된다. 조건에 따르면 회의가 끝나는 시간과 시작 시간이 같을 수도 있으므로, 선택한 회의의 시작 시간이 이전 회의의 종료 시간과 같거나 커야 한다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
bool compare(pair<int,int> a, pair<int,int> b)
{
if (a.second == b.second) {
return a.first < b.first;
}
return a.second < b.second;
}
int main()
{
int n;
cin >> n;
vector < pair<int, int > > a(n);
for (int i = 0; i < n; i++) {
cin >> a[i].first >> a[i].second;
}
sort(a.begin(), a.end(), compare);
int ans = 1;
int temp = a[0].second;
for (int i = 1; i < n; i++) {
if (a[i].first >= temp) {
ans += 1;
temp = a[i].second;
}
}
cout << ans << '\n';
return 0;
}- 예제처럼 정렬되어 값이 주어지면 좋겠지만, 문제에 따로 조건이 없으므로 입력 받은 값을 먼저 정렬해준다. 기준은 종료 시간으로, 종료 시간이 같으면 시작 시간을 기준으로 오름차순 정렬한다. 그 다음 생각한대로 구현해주면 된다.
* ATM (low) : 모든 사람이 인출까지 걸리는데 필요한 시간의 합을 최소로 만드는 문제다.
11399번: ATM
첫째 줄에 사람의 수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 각 사람이 돈을 인출하는데 걸리는 시간 Pi가 주어진다. (1 ≤ Pi ≤ 1,000)
www.acmicpc.net
- 각각 인출에 걸리는 시간이 다르고 줄을 서서 인출을 한다. 그럼 뒷사람이 인출에 걸리는 시간에는 앞사람이 인출하는데 걸리는 시간이 더해질 수 밖에 없다.
- 맨 앞의 사람이 걸리는 시간은 그 뒤에 사람에게 영향을 주고, 또 그 다음은 그 뒤에 영향을 주고 하니까.. 그럼 맨 앞에 있는 사람이 가장 적은 시간이 걸리도록 정렬해주면 되겠다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int n;
cin >> n;
vector<int> p(n);
for (int i = 0; i < n; i++)
cin >> p[i];
sort(p.begin(), p.end());
int ans = 0;
int time = 0;
for (int i = 0; i < n; i++) {
time += p[i];
ans += time;
}
cout << ans << '\n';
return 0;
}- 오름차순 정렬하고 소요 시간을 누적해서 더해주면 된다.
* 행렬 (mid) : 행렬 A를 B로 바꾸는데 필요한 연산의 최솟값을 구하는 문제다.
1080번: 행렬
첫째 줄에 행렬의 크기 N M이 주어진다. N과 M은 50보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 행렬 A가 주어지고, 그 다음줄부터 N개의 줄에는 행렬 B가 주어진다.
www.acmicpc.net
- 여기서 말하는 연산은 어떤 3*3 크기의 부분 행렬에 있는 모든 원소를 뒤집는 거다. 0은 1, 1은 0이 된다.
- 이것도 그림을 그려서 생각하면 이해가 빠르다.
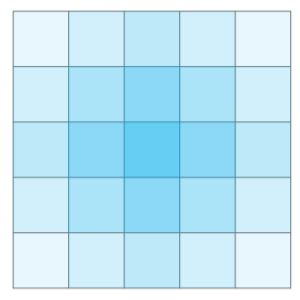
- 연산이 가능한 범위를 색칠해서 나타낸 건데, 핵심은 순서대로 연산을 했을 때 가장 왼쪽 위의 연산은 항상 마지막 연산이 된다는 거다. 그러니까 그리디를 이용해서 가장 왼쪽 위의 값이 B와 다르면 연산을 해주는 식으로 진행하면 된다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstdio>
using namespace std;
int n, m;
int a[50][50], b[50][50];
void change(int x, int y) {
for (int i = x; i < x + 3; i++) {
for (int j = y; j < y + 3; j++) {
a[i][j] = 1 - a[i][j];
}
}
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
scanf("%1d", &a[i][j]);
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
scanf("%1d", &b[i][j]);
}
}
int ans = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (i + 2 <= n - 1 && j + 2 <= m - 1) {
if (a[i][j] != b[i][j]) {
change(i,j);
ans += 1;
}
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (a[i][j] != b[i][j]) {
cout << -1 << '\n';
return 0;
}
}
}
cout << ans << '\n';
return 0;
}- 해당 위치의 값이 연산 가능한 범위 내에 있고, 구하려는 행렬의 같은 위치의 값과 다르면 연산을 해준다.
* 전구와 스위치 (mid) : 위의 행렬 문제를 조금 다른 방식으로 제시한 문제다.
2138번: 전구와 스위치
N개의 스위치와 N개의 전구가 있다. 각각의 전구는 켜져 있는(1) 상태와 꺼져 있는 (0) 상태 중 하나의 상태를 가진다. i(1<i<n)번 스위치를="" 누르면="" i-1,="" i,="" i+1의="" 세="" 개의="" 전구의="" 상태가="" 바뀐다.="" 즉,="" 꺼��<="" p=""> </i<n)번>
www.acmicpc.net
- 이것도 그림을 그려보면 이해가 빠르다.

- 위의 행렬 문제에서는 가장 위의 왼쪽이 마지막 연산이 된다는 것을 바로 알 수 있었는데, 여기는 마지막 연산이 될 수 있는 게 바로 보이지 않는다. 그럼 보이게 만들면 된다.
- 가장 왼쪽의 스위치의 상태가 결정이 되면, 그 뒤의 스위치가 마지막 선택이 된다는 것을 알 수 있다. 그 뒤부터는 연쇄적으로 가장 왼쪽의 상태를 결정할 수 있다.

- 따라서 가장 왼쪽의 상태가 결정되고, i번째 스위치 선택을 할 때, i-1번째 전구가 구하고자 하는 전구의 상태와 다르면 스위치를 눌러 값을 같게 만들어줘야 한다. 가장 왼쪽 스위치를 눌렀을 때와 안 눌렀을 때로 나눠서 생각하면 된다.
- 알고리즘을 이해하긴 했는데, 깔끔하게 코딩이 잘 안 되는 느낌이어서 정답 코드를 많이 참고했다. (거의 똑같)
#include <vector>
#include <cstdio>
#include <algorithm>
using namespace std;
void change(vector <int> &a, int idx) {
for (int i = idx - 1; i <= idx + 1; i++) {
if (i < 0 || i >= a.size()) continue;
a[i] = 1 - a[i];
}
}
pair<bool, int> go(vector<int> a, vector<int> b) {
int n = a.size();
int cnt = 0;
for (int i = 1; i < n; i++) {
if (a[i - 1] != b[i - 1]) {
change(a, i);
cnt += 1;
}
}
if (a == b) {
return make_pair(true, cnt);
}
else {
return make_pair(false, -1);
}
}
int main()
{
int n;
scanf("%d", &n);
vector<int> a(n), b(n);
for (int i = 0; i < n; i++) {
scanf("%1d", &a[i]);
}
for (int i = 0; i < n; i++) {
scanf("%1d", &b[i]);
}
auto p1 = go(a, b);
change(a, 0);
auto p2 = go(a, b);
p2.second += 1;
if (p1.first && p2.first) {
printf("%d\n", min(p1.second, p2.second));
}
else if (p1.first) {
printf("%d\n", p1.second);
}
else if (p2.first) {
printf("%d\n", p2.second);
}
else {
printf("-1\n");
}
return 0;
}- p1에는 가장 왼쪽 스위치를 안 눌렀을 때, p2에는 눌렀을 때의 상태가 들어간다. 각각 연산을 마쳤을 때, 전구의 상태가 같은지, 같다면 스위치를 몇번 눌렀는지를 리턴한다. 둘 다 가능하다면 그 중 최솟값을 구해주면 된다.
* 동전 뒤집기 (mid) : 앞과 같은 맥락의 문제였다. 근데 고려해야 하는 범위가 커서 생각을 잘 해줘야 했다.
1285번: 동전 뒤집기
첫째 줄에 20이하의 자연수 N이 주어진다. 둘째 줄부터 N줄에 걸쳐 N개씩 동전들의 초기 상태가 주어진다. 각 줄에는 한 행에 놓인 N개의 동전의 상태가 왼쪽부터 차례대로 주어지는데, 앞면이 위�
www.acmicpc.net
- 가장 단순하게 생각하면 모든 행, 열을 뒤집거나 안 뒤집을 때를 생각해서 T의 최솟값을 구해주면 된다. 그렇게 구하면 n이 20이하이므로 시간 복잡도는 거의 O(2^40)에 육박한다.
- 먼저 행만 뒤집거나 안 뒤집을 때를 생각해주고, 열은 T값과 H값 중에 작은 값을 취하고 누적해서 더해주면 현재 상태에서 T의 최솟값을 구할 수 있다. 굳이 뒤집어주는 연산을 하지 않아도, 현재 열의 T 개수가 H 개수보다 크다면 현재의 H 개수가 T 개수라고 생각해주면 된다.
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
char flip(char x) {
if (x == 'H') return 'T';
else return 'H';
}
int main()
{
int n;
cin >> n;
vector<string> a(n);
for (int i = 0; i < n; i++)
cin >> a[i];
vector<string> temp = a;
int ans = n*n;
for (int state = 0; state < (1 << n); state++) { // 행의 상태
int sum = 0;
for (int j = 0; j < n; j++) { // 열
int cnt = 0;
for (int i = 0; i < n; i++) { // 행
char cur = a[i][j];
if (state & (1 << i)) { // 뒤집는 행이면
cur = flip(cur); // 뒤집어
}
if (cur == 'T') { // T를 카운트 해주고
cnt += 1;
}
}
sum += min(cnt, n - cnt); // T, H 중에 작은 거 (열을 뒤집거나 안 뒤집거나)
}
if (ans > sum) ans = sum;
}
cout << ans << '\n';
return 0;
}- 풀이 방향은 잡았는데 알고리즘 구현이 좀 까다로워서 정답 코드를 참조했다. 근데 정말 이런 코드는 못 짰을 것 같더라.
- 먼저 행의 상태를 비트 마스크를 이용해 잡아주고, 열을 기준으로 반복문을 돌려준다. 해당 위치의 값을 먼저 취한 뒤에, 이 행이 뒤집히는 행이면 flip 함수를 이용해 뒤집어준다. 그 다음 T값을 카운트 해준다.
- 한 열의 연산이 끝나면 T값을 카운트한 cnt와 n-cnt 중 최솟값을 누적해서 더해준다. T의 개수가 H의 개수보다 적으면 아무 연산 없이 cnt를 취하는 것이고, T 개수가 H 개수보다 많으면 열을 뒤집어 n-cnt를 취하는 것이다.
- 모든 열의 연산이 끝나면 T의 개수를 누적해서 더한 값을 갱신해준다.
- 보고 좀 멍했던 알고리즘이었다. 언제쯤 이런 알고리즘 센스를 발휘할 수 있을지.. 갈 길이 멀다.
-
결심한 대로 진도가 빨라졌다. 할 게 많다. 더 빡세게 해봐야겠다.
정리 끝!
'알고리즘 > 백준 알고리즘 강의' 카테고리의 다른 글
| 백준 알고리즘 중급 - 그리디 알고리즘 (연습) (0) | 2020.08.26 |
|---|---|
| 백준 알고리즘 중급 - 그리디 알고리즘 - 2 (0) | 2020.08.25 |
| 백준 알고리즘 중급 - BFS (연습) - 2 (0) | 2020.08.24 |
| 백준 알고리즘 중급 - BFS (연습) - 1 (0) | 2020.08.18 |
| 백준 알고리즘 중급 - 브루트 포스 : 비트마스크 (연습) (0) | 2020.08.14 |



